About the figures


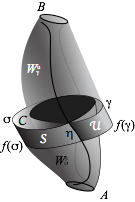
(Courtesy of Jim Meiss) Stable and unstable manifolds of a pair of saddle fixed points of the quadratic volume preserving automorphism. See Lomelí, H. E. and J. D. Meiss (1998). “Quadratic volume-preserving maps.” Nonlinearity 11(3): 557-574. <http://iopscience.iop.org/0951-7715/11/3/009/>
(Courtesy of Jim Meiss) Construction of a partial barrier from stable and unstable manifolds of a pair of invariant circles of a volume preserving map. See Lomelí, H. E. and J. D. Meiss (2009). “Resonance Zones and Lobe Volumes for Volume-Preserving Maps.” Nonlinearity 22: 1761-1789. <http://www.iop.org/EJ/abstract/0951-7715/22/8/001/>
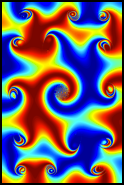
(Courtesy of Per Sebastian Skardal) Each pixel represents the sine of a phase oscillator (red = 1, blue = -1) which is coupled sinusoidally to those around it. Spiral waves form spontaneously due to a slight phase lag in the coupling function. Even though all oscillators are nearly identical, coexisting regions of both coherent (e.g. spirals) and incoherent (e.g. central core) form. Similar systems have been studied in C. R. Laing, Phys. D 238, 1569 (2009) and E. A. Martens, C. R. Laing, and S. H. Strogatz, Phys. Rev. Lett 104, 044101 (2010).
(Courtesy of Pat Weidman) Helical instability modes for a rotating viscous jet. For more information, see J. P. Kubitschek and P. D. Weidman, J. Fluid Mech. vol. 572, pp. 261–286 (2007), and Physics of Fluids vol. 19, p. 114108 (2007).
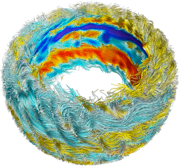
(Courtesy of Benjamin Brown and Juri Toomre) Magnetic wreaths in the convection zone of a solar-type star. The equatorial region is highlighted here, and color gives the polarity of the magnetic fields. See also http://jila.colorado.edu/content/spinning-out-starspots and references therein.